


Next: Track C: Experimentation
Up: Methodology
Previous: Track A: The Typed
This track extends the theory of quantitative secrecy analysis in
[25] to the linear/affine typed 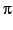 -calculus.
Concurrently we extend the qualitative secrecy analysis in
[45,41,46,75,68] to the enriched linear/affine
-calculus.
Concurrently we extend the qualitative secrecy analysis in
[45,41,46,75,68] to the enriched linear/affine
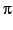 -calculus from Track A. Concretely:
-calculus from Track A. Concretely:
- (a) Quantitative Secrecy Analysis.
- We first extend the
semantics of the
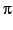 -calculus using probabilistic transition
systems along the line of [25]. This is then
instantiated syntactically, resulting in the probabilistic typed
-calculus using probabilistic transition
systems along the line of [25]. This is then
instantiated syntactically, resulting in the probabilistic typed
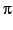 -calculus. The interplay between probability and
sophisticated typing is the main technical challenge of this part.
Once a consistent calculus is developed, we develop a theory of
secrecy on the basis of [25], which may possibly assisted
by the idea of flow inference in [46]. Once a semantic basis
is clearly understood, we develop a syntactic, compositional method
for qualitative secrecy, and reflect it onto programming
languages of sufficient complexity.
-calculus. The interplay between probability and
sophisticated typing is the main technical challenge of this part.
Once a consistent calculus is developed, we develop a theory of
secrecy on the basis of [25], which may possibly assisted
by the idea of flow inference in [46]. Once a semantic basis
is clearly understood, we develop a syntactic, compositional method
for qualitative secrecy, and reflect it onto programming
languages of sufficient complexity.
- (b) Qualitative Secrecy Analysis.
- We extend the secrecy
analyses in [45,41,46,75,68] to the enriched typed
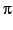 -calculus from Track A in two steps. First, we develop flow
inference systems as well as their semantic basis following
[46]. This leads to a clear
understanding of information flows in the enriched type structure, as shown in
[46]. Second, based on the insights obtained, we enrich
the secrecy typing in [45] for accommodating the new type
structure. Finally we check that the resulting typing is consistent
with the flow inference in [46], leading to non-interference.
-calculus from Track A in two steps. First, we develop flow
inference systems as well as their semantic basis following
[46]. This leads to a clear
understanding of information flows in the enriched type structure, as shown in
[46]. Second, based on the insights obtained, we enrich
the secrecy typing in [45] for accommodating the new type
structure. Finally we check that the resulting typing is consistent
with the flow inference in [46], leading to non-interference.



Next: Track C: Experimentation
Up: Methodology
Previous: Track A: The Typed
Igor Siveroni
2004-08-16
![]() -calculus.
Concurrently we extend the qualitative secrecy analysis in
[45,41,46,75,68] to the enriched linear/affine
-calculus.
Concurrently we extend the qualitative secrecy analysis in
[45,41,46,75,68] to the enriched linear/affine
![]() -calculus from Track A. Concretely:
-calculus from Track A. Concretely: