


Next: Track B: Qualitative/Quantitative Security
Up: Methodology
Previous: Methodology
This track extends the linear/affine typed 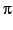 -calculus
so that it can faithfully represent major classes of
language constructs, building on our preceding work [12,72].
The results serve as a mathematical basis of the present project, and
is obtained via the following three steps.
-calculus
so that it can faithfully represent major classes of
language constructs, building on our preceding work [12,72].
The results serve as a mathematical basis of the present project, and
is obtained via the following three steps.
- Identification of the type structure and typing rules for that
language class (say sequential imperative computation).
- Encoding of some programming languages belonging to that
class into the calculus, establishing well-typedness.
- Establishment of equational full abstraction of the embedding,
showing equations over programs in the source language coincides
with those over the encoding in the calculus. One of the key
arguments is so-called definability, which establishes a tight
correspondence between the object language and the co-domain of its
embedding.
These steps have already been applied to the basic linear/affine
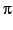 -calculus [12,72,45,,,75], which will now be
extended to a wider class of computational behaviours
encompassing, for example, a major part of Java.
-calculus [12,72,45,,,75], which will now be
extended to a wider class of computational behaviours
encompassing, for example, a major part of Java.
Igor Siveroni
2004-08-16
![]() -calculus
so that it can faithfully represent major classes of
language constructs, building on our preceding work [12,72].
The results serve as a mathematical basis of the present project, and
is obtained via the following three steps.
-calculus
so that it can faithfully represent major classes of
language constructs, building on our preceding work [12,72].
The results serve as a mathematical basis of the present project, and
is obtained via the following three steps.