


Next: Construction of Analyses.
Up: Programme and Methodology
Previous: Quantitative Semantics.
PAI has been introduced in [21,22] as a probabilistic version
of the classical abstract interpretation framework introduced by Cousot &
Cousot. Given two probabilistic domains, 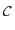 and
and 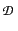 , a probabilistic
abstract interpretation is a pair of linear maps,
, a probabilistic
abstract interpretation is a pair of linear maps,
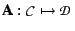 and
and
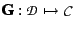 , between the concrete domain
, between the concrete domain 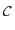 and the abstract
domain
and the abstract
domain 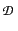 , such that
, such that 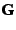 is the Moore-Penrose pseudo-inverse of
is the Moore-Penrose pseudo-inverse of 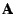 ,
and vice versa. The Moore-Penrose pseudo-inverse is defined as follows: Let
,
and vice versa. The Moore-Penrose pseudo-inverse is defined as follows: Let
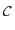 and
and 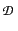 be two vector spaces and
be two vector spaces and
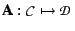 a linear map between them. A linear map
a linear map between them. A linear map
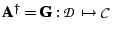 is the Moore-Penrose pseudo-inverse of
is the Moore-Penrose pseudo-inverse of 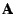 iff
iff
where 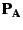 and
and 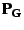 denote orthogonal projections onto the ranges of
denote orthogonal projections onto the ranges of
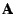 and
and 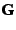 . The projections are idempotent and self-adjoint; as a
consequence, we can derive analogues of many of the properties of Galois
connections that are used in the classical theory of abstract interpretation.
A simple method to construct a probabilistic abstract interpretation is as
follows. Given a linear operator
. The projections are idempotent and self-adjoint; as a
consequence, we can derive analogues of many of the properties of Galois
connections that are used in the classical theory of abstract interpretation.
A simple method to construct a probabilistic abstract interpretation is as
follows. Given a linear operator 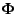 on some vector space
on some vector space 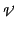 expressing
the probabilistic semantics of a concrete system, and a linear abstraction
function
expressing
the probabilistic semantics of a concrete system, and a linear abstraction
function
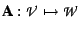 from the concrete domain into an abstract domain
from the concrete domain into an abstract domain
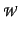 , we compute the (unique) Moore-Penrose pseudo-inverse
, we compute the (unique) Moore-Penrose pseudo-inverse
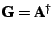 of
of 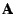 . The abstract semantics can then be defined as the linear operator
on the abstract domain
. The abstract semantics can then be defined as the linear operator
on the abstract domain 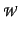 :
:
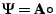
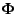
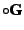 .
.



Next: Construction of Analyses.
Up: Programme and Methodology
Previous: Quantitative Semantics.
Igor Siveroni
2004-08-12